本文共 7792 字,大约阅读时间需要 25 分钟。
文章目录
数据库的完整性
- 数据的正确性:数据是符合现实世界语义,反映了当前实际状况的
- 数据的相容性:同一对象在不同关系表中的数据是符合逻辑的
数据的完整性
防范对象:不合语义的、不正确的数据 数据的安全性 防范对象:非法用户和非法操作一、实体完整性
1 实体完整性定义
[例5.1] 将Student表中的Sno属性定义为码
--方式一:在列级定义主码create table Student(Sno char(20) primary key, --在列级定义主码 Sname char(10) not null, Ssex char(2), Sage int, Sdept char(5));-- 方式二:在表级定义主码create table Student(Sno char(20), Sname char(10) not null, Ssex char(2), Sage int, Sdept char(5), primary key(Sno));
例2:将SC表中的Sno、Cno属性定义为主码
create table SC(Sno char(20), Cno char(4), Grade int, primary key(Sno,Cno), -- 在表级定义主码,主码中包含多个属性);
2.实体完整性检查和违约处理
插入或更新操作时,DBMS按照实体完整性规则自动进行检查。
- 检查主码值是否唯一,如果不唯一则拒绝插入或修改。
- 检查主码的各个属性是否为空,只要有一个为空就拒绝插入或修改
- 借用之前的实验数据,填充Student 表
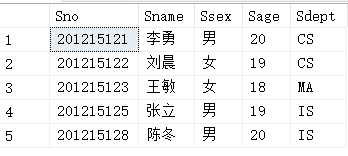 学号是主键,重复了。出入被禁止
学号是主键,重复了。出入被禁止
insert into Student values('201215121','李强','男',20,'CS');  填充SC表
填充SC表
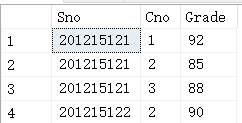 当主码中的属性是重复的时候也不被允许,违反了主键约束
当主码中的属性是重复的时候也不被允许,违反了主键约束 insert into SC values ('201215121','2',95) 
二、参照完整性
1.定义参照完整性
关系模型的参照完整性定义
- 在CREATE TABLE中用FOREIGN KEY短语定义哪些列为外码
- 用REFERENCES短语指明这些外码参照哪些表的主码
[例5.3]定义SC中的参照完整性
create table SC(Sno char(20), Cno char(4), Grade int, primary key(Sno,Cno), -- 在表级定义实体完整性 foreign key(Sno) references Student(Sno),-- 在表级定义参照完整性 foreign key(Cno) references Course(Cno) -- 在表级定义参照完整性);
可能破坏参照完整性的情况及违约处理
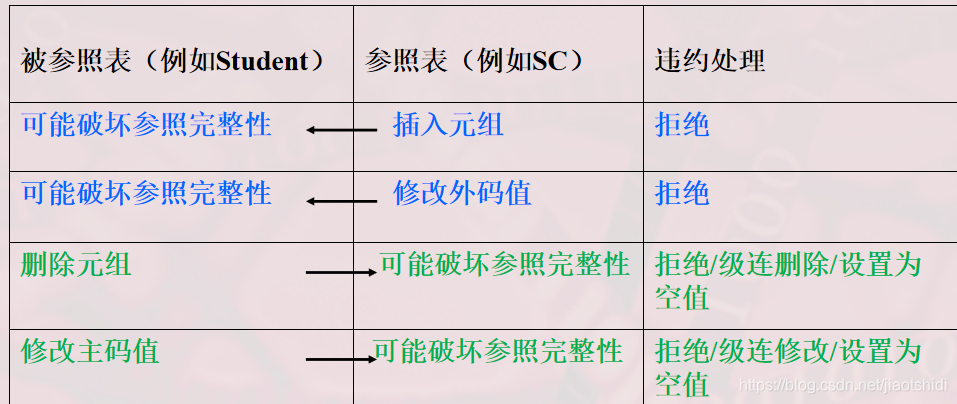 [例5.4] 显式说明参照完整性的违约处理示例
[例5.4] 显式说明参照完整性的违约处理示例 create table SC(Sno char(20), Cno char(4), Grade int, primary key(Sno,Cno), foreign key(Sno) references Student(Sno) on delete cascade -- 级联删除SC表中相应的元组 on update cascade, -- 级联更新SC表中相应的元组 foreign key(Cno) references Course(Cno) on delete no action -- 当删除Course表中的元组造成与SC表不一致时,拒绝删除 on update cascade -- 当更新Course表中的Cno时,级联更新SC表中相应的元组 );
三、用户自定义的完整性
用户定义的完整性是:针对某一具体应用的数据必须满足的语义要求
属性上的约束条件
CREATE TABLE时定义属性上的约束条件
- 列值非空(NOT NULL)
- 列值唯一(UNIQUE)
- 检查列值是否满足一个条件表达式(CHECK)
[例5.5] 在定义SC表时,说明Sno、Cno、Grade属性不允许取空值。
create table SC(Sno char(20), Cno char(4), Grade int , primary key(Sno,Cno), -- 在表级定义实体完整性,隐含了Sno,Cno不允许取空值,在列级不允许取空值的定义可不写);
[例5.6]建立部门表DEPT,要求部门名称Dname列取值唯一,部门编号Deptno列为主码
create table DEPT(Deptno numeric(2),Dname char(9) unique not null,Location char(10),primary key(Deptno));
[例5.7] Student表的Ssex只允许取“男”或“女”。
create table Student(Sno char(20) primary key,Sname char(10) not null,Ssex char(2) check (Ssex in('男','女')), --性别属性只能取男或女Sage int,Sdept char(5)); [例5.8] SC表的Grade的值应该在0和100之间。
create table SC(Sno char(20),Cno char(4),Grade int check(Grade>=0 and Grade<=100),primary key(Sno,Cno),foreign key(Sno)references Student(Sno),foreign key(Cno)references Course(Cno));
属性上的约束条件检查和违约处理
- 插入元组或修改属性的值时,关系数据库管理系统检查属性上的约束条件是否被满足
- 如果不满足则操作被拒绝执行
2 元组上的约束条件
在CREATE TABLE时可以用CHECK短语定义元组上的约束条件,即元组级的限制
[例5.9]当学生的性别是男时,其名字不能以Ms.打头。
create table Student ( Sno char(9), Sname char(8) not null, Ssex char(2), Sage smallint, Sdept char(20), primary key (Sno), check (Ssex='女' or Sname not like 'Ms.%')--定义了元组中Sname和 Ssex两个属性值之间的约束条件 );
元组上的约束条件检查和违约处理和属性上的类似
四、 完整性约束命名子句
优点是方便在建立表之后的对约束条件进行增删改
1.完整性约束命名子句
CONSTRAINT <完整性约束条件名> <完整性约束条件>
<完整性约束条件>包括NOT NULL、UNIQUE、PRIMARY KEY短语、FOREIGN KEY短语、CHECK短语等
[例5.10]建立学生登记表Student,要求学号在90000~99999之间,姓名不能取空值,年龄小于30,性别只能是“男”或“女”。
create table Student ( Sno numeric(6) constraint C1 check (Sno between 90000 and 99999), Sname char(20) constraint C2 NOT NULL, Sage numeric(3) constraint C3 check (Sage < 30), Ssex char(2) constraint C4 check(Ssex in( '男','女')), constraint StudentKey primary key(Sno) );
[例5.11]建立教师表TEACHER,要求每个教师的应发工资不低于3000元。应发工资是工资列Sal与扣除项Deduct之和。
create table TEACHER ( Eno numeric(4) primary key, /*在列级定义主码*/ Ename char(10), Job char(8), Sal numeric(7,2), Deduct numeric(7,2), Deptno numeric(2), constraint TEACHERFKry foreign key (Deptno) references DEPT(Deptno), constraint C1 check(Sal + Deduct >= 3000) --应发工资是工资列Sal与扣除项Deduct之和。 );
2. 修改表中的完整性限制
[例5.12]去掉例5.10 Student表中对性别的限制。
alter table Student drop constraint C4;
[例5.13] 修改表Student中的约束条件,要求学号改为在900000~999999之间,年龄由小于30改为小于40
alter table Studentdrop constraint C1;alter table Studentadd constraint C1 check(Sno between 900000 and 999999);alter table Studentdrop constraint C3;alter table Studentadd constraint C3 check(Sage<40);--这里都是先删除再增加以达到改变的目的
五、 断言
SQL中,可以使用 CREATE ASSERTION语句,通过声明性断言来指定更具一般性的约束。
- 可以定义比较复杂的完整性约束。
- 断言创建以后,任何对断言中所涉及的关系的操作都会触发DBMS对断言的检查,任何使断言不为真值的操作都会被拒绝执行
创建断言的语句格式
CREATE ASSERTION<断言名><CHECK 子句>
[例5.18] 限制数据库课程最多60名学生选修
create assertion ASSE_SC_DB_NUM check (60 >= (select count(*) from Course,SC where SC.Cno=Course.Cno and Course.Cname ='数据库') );
[例5.19]限制每一门课程最多60名学生选修
create assertion ASSE_SC_CNUM1check(60 >= all (select count(*) from SC group by cno) );
2.删除断言的语句格式
drop assertion <断言名>
六、触发器
1、定义触发器
CREATE TRIGGER语法格式CREATE TRIGGER <触发器名> {BEFORE | AFTER} <触发事件> ON <表名> REFERENCING NEW|OLD ROW AS <变量> FOR EACH { ROW | STATEMENT}[WHEN <触发条件> ] <触发动作体> 行级触发器(FOR EACH ROW)
语句级触发器(FOR EACH STATEMENT)2.触发事件
[例5.21]当对表SC的Grade属性进行修改时,若分数增加了10%则将此次操作记录到下面表中:
标准SQL
create trigger SC_Tafter update of Grade on SCreferencing old row as OldTuple, new row as NewTuplefor each rowwhen (NewTuple.Grade>=1.1*OldTuple.Grade)insert into SC_U(Sno,Cno,OldGrade,NewGrade)values(OldTuple.Sno,OldTuple.Cno,OldTuple.Grade,NewTuple.Grade);
TSQL
需要先声明变量,实现声明好需要插入的新变量,用到 @符号声明变量,用insert 和 deleted来区分更新前后的数据,还需要用到begin和endcreate trigger SC_Ton SCafter updateasbegin declare @old int,@new int,@sno char(15),@cno char(10) if(update(Grade)) begin select @old=Grade from deleted select @new=Grade from inserted select @sno=Sno from inserted select @cno=Cno from inserted if(@new>=1.1*@old) insert into SC_U(Sno,Cno,Old,New) values(@sno,@cno,@old,@new) endend;
检验测试样例
update SCset Grade=50where Sno='201215121' and Cno='2';select * from SC_U
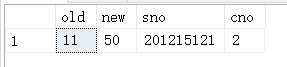
[例5.22] 将每次对表Student的插入操作所增加的学生个数记录到表StudentInsertLog中。
标准SQL
create trigger Student_Countafter insert on Student new table as Delta for each statement insert into Studentinsertlog(Numbers) select count(*) from delta;
TSQL
create table StudentInsertLog(Numbers int);--分开写 create trigger Student_Counton Studentafter insertas insert into StudentInsertLog(Numbers)select count(*) from Student;
[例5.23] 定义一个BEFORE行级触发器,为教师表Teacher定义完整性规则“教授的工资不得低于4000元,如果低于4000元,自动改为4000元”。
create trigger insert_or_Update_Salbefore insert or update on Teacherfor each rowbegin if(new.Job='教授')and(new.sal<4000)then new.Sal :=4000;end if;end;
4.激活触发器
触发器的执行,是由触发事件激活的,并由数据库服务器自动执行!
一个数据表上可能定义了多个触发器,遵循如下的执行顺序:
(1) 执行该表上的BEFORE触发器;
(2) 激活触发器的SQL语句;
(3) 执行该表上的AFTER触发器
5.删除触发器
DROP TRIGGER <触发器名> ON <表名> ;
七、存储过程和函数
存储过程:由过程化SQL语句,经编译和优化后存储在数据库服务器中,可以被反复调用,运行速度较快。
优点:
(1)运行效率高
(2)降低了客户机和服务器之间的通信量
(3)方便实施企业规则
1、创建存储过程
CREATE OR REPLACE PROCEDURE 过程名([参数1,参数2,...]) AS <过程化sql块> ;
[例8.8] 利用存储过程来实现下面的应用:从账户1转指定数额的款项到账户2中。
create procedure Proc_TRANSFER (--定义存储过程为 transfer@inAccount int,@outAccount int,@amount float)--形参asbegin transaction transdeclare@totalDepositOut float,--定义变量@totalDepositin float,@inAccountum int; select @totalDepositOut=total from Account where accountnum = @outAccount;if @totalDepositOut is null --1.如果转出账户不存在或账户中没有存款begin print '转出账户不存在或者账户余额为0'rollback transaction trans; --回滚事务returnend ;if @totalDepositOut < @amount --2.账户余额不足begin print '账户余额不足'rollback transaction trans;return;end select @inAccount =accountnum from Accountwhere accountnum = @inAccount;if @inAccount is nullbeginprint '转入账户不存在'rollback transaction trans;return ;end ;beginupdate Account set total =total-@amountwhere accoutnum =@outAccount;update account set total = total+@amountwhere accountnum =@inAccount;print '转账成功'commit transaction trans;return ;end;
2、执行存储过程
[例8.9] 从账户01003815868转10000元到01003813828账户中。
call proceduretransfer (01003813828,01003815868,10000);
TSQL
exec Proc_TRANSFER@inAccount = 01003813828, --转入账户@outAccount = 01003815868, --转出账户@amount = 10000 --转出金额select * from Account;
3、修改存储过程
alter procedure 过程名1 rename to 过程名2;
4、删除存储过程
drop procedure 过程名();
转载地址:http://ffvx.baihongyu.com/